P1（微分几何函数求解）

本题考查的分别是第二章二次函数如何求解，第五章如何求直线方程以及两直线垂直斜率相乘得-1这个知识点，还有第八章微分的几何意义：导数的几何意义就是曲线上某点处切线的斜率。通过微分求出斜率求出切线方程。也就是说这道题其实没有单纯的考一个知识点或者一个章节，而是从三个章节中选出常考的知识点进行结合，这也是我们在考试中经常会出现的考法：多个章节的知识点结合出题。

那么a问就是证明P点在曲线C上，只需要证明P点的x,y坐标可以满足曲线方程就好，因为它既然在曲线上就是C上无数个点中的一员，所以我们需要做的就是将P点的坐标带入进曲线的方程里。b问要求的是曲线上P点的切线，既然要求直线就要知道直线的方程，利用点斜式直线方程(点斜式方程只需要一个点和斜率，这里我们已知P点坐标，只再需要一个斜率就好)，求斜率，斜率的求法就是根据我们微分一章学到的几何意义，求导得到的就是曲线上任意一点的斜率，无数个点有无数个切线以及斜率，区别的点就在于点的坐标，所以我们将P点坐标带入到求出的导数里面就可以求出该条切线的斜率，最后连同P点带入到直线方程，得到tangent(切线)。最后一问给了额外的条件：曲线C上Q点的切线和P点的切线垂直，读到这句话就可以得出两直线的斜率关系：相乘得-1。根据P切线的斜率得到Q直线的斜率，那么前面我们提到斜率就是曲线的导数，所以我们只需要利用求完的导数和P的导数互为负导数就可以了，最后得都Q点的横坐标。

该学生a问是按照老师的要求去把点带入到曲线里了，b问也是先通过求导带入点进去得到斜率，再把斜率点带入到直线就可以了。所以这两问都得到分数了，最后一问就是对于二次函数以及导数的定义不够清晰，所以不会求解。

该学生解题思路清晰且步骤书写工整，说明对题目理解比较到位，所以得分也比较容易。

P2 (数列应用题)

这是P2的一道关于数列的应用题，需要同时掌握等差等比数列的公式应用，同时这是在纯数里面对英文要求相对较高的一道题目。

首先Model 1是每天比前一天增长1000，所以这是一个等差数列，因为我们要得到前40天的总额，所以我们用到的是求和公式。

Model 2 是每天相对前一天增长10%，这就是一个等比数列，但是要注意的是我们在用公式的时候其中的r是110%，即需要考虑到本身是有1倍，增加10%，就是原来的1.1倍。

但是这题的最后我们要审题，因为我们要把总额的5%捐出去，所以最后要乘一下。

下面我们来看一下学生的答题情况

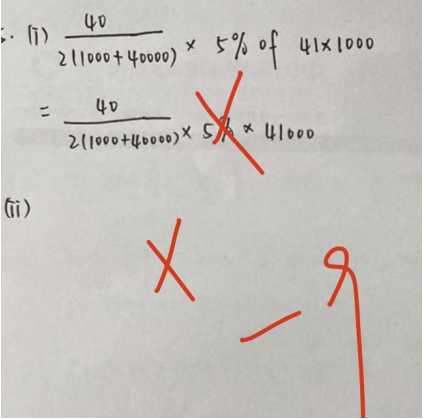
位同学很明显没有理解公式怎么用，我们等差等比求和公式分别如下：

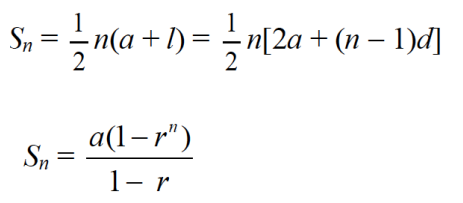
Model1中 n是天数：40，a为天的钱：1000，d为每天增加的数：1000。把每个数值带入变量即可求出前40天总和。

Model2中其他变量一样，r为增长比例是1.1

最后分别乘以5%就是最后结果。

第二位学生表现的就比较好，但是在最后等比的计算中我们的n还是40，学生写成了39。

在这类题目计算时，大家要注意先运用求和公式再乘以5%，这样不容易出错。

学生在考试中需要注意审题，计算要仔细，如果时间充分，检查多次，避免失误。