SAT数学重要知识点：概率Probabilities

　　概率，说的是事件发生的可能性，其数值在0到1之间。概率为0的事件叫做“不可能事件”。概率为1的事件叫做“必然事件”。其他的事件叫做“或然事件”。可以被计算的概率，在SAT的考核中常常是古典概型。

　　1.古典概型

　　古典概型是最简单最常见的概率。它说的是：同一时间可以有n个事件发生，每个事件发生的可能性都是相等的。因此，我们所要求的目标事件发生的可能性，就是(目标事件)/(总事件)。

　　比方说，在一个罐子里面有19块红糖，15块白糖。随机抽取一块糖，该糖是红糖的可能性(概率)就是19/(19+15)=19/34。见如下例题1(Official Guide的题目)：

　　例题1：

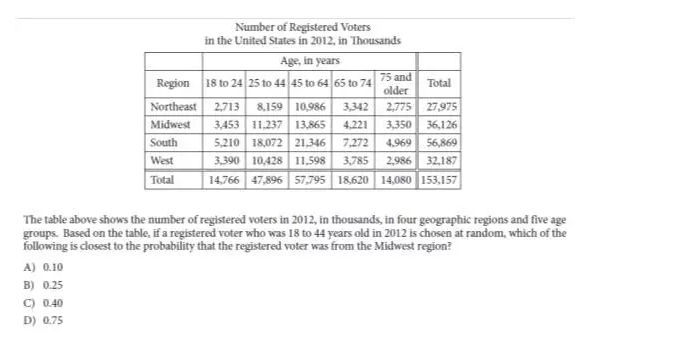
　　解析：表面上看，这是一道图表分析题。但是看到实质你会发现这是有关于概率的一道题目。题目里面首先圈定了范围“18-44岁的选民”，这应该是(14766+47896)人，而其中来自Midwest的人是(3453+11237)人，因此，所求的概率就是： (3453+11237)/ (14766+47896)=14690/62662=0.234，因此选择B。

　　事实上，以图表形式来考核的古典概型的题目很多，几乎每次考试中都会遇到。 但是有的时候，考核的内容不是单一事件，而且很多事件结合在一起的概率。因此，必须要先熟悉这几个概念和公式。

　　请看下面的例题2：

　　例题2(Official Guide的题目)：

　　解析：probability of either AorB说明了要求的是两个事件的并集，即：两个事件中只要有一件事发生即可。

　　而“female under40”和“male40 or older”是两个互斥事件，没有人可以即是40岁以下的女人同时又是40岁以上的男人。因此，这个概率就是两个单独的事件的概率的叠加，即：P(AUB)=P(A)+P(B)，因此答案选择B。

　　3.条件概率

　　条件概率说的就是事件A在事件B已经发生的情况下而发生的概率，表达为P(A|B)。

　　那么，如果一件事件的发生可能性不受另一件事发生与否的影响，这两件事情就叫做互相独立的事件，表达为：P(A)=P(A|B),则AB互相独立。同样，也有P(B)=P(B|A)的表达。

　　对于互斥事件，我们知道：一件事发生，另外一件事就一定不会发生，因为他们是互斥的，所以表达为：P(A)>0,但是P(A|B)=0。

　　如果两件事情并不能保证互相独立，则一件事情的条件概率的表达方式如下：

　　P(A|B)=P(AB)/P(B)。

　　对于条件概率的表达和计算，可以通过这样一道题目来简单理解：一个盒子里面有20块糖，其中12块白色的，8块黄色的。在12块白色糖中，有5块白巧克力糖。求：(1)随机抽取一块糖是白巧克力糖的概率;(2)如果随机抽取一块糖是白色的糖，求该糖是白巧克力糖的概率。

　　解：(1)就是古典概型的题目。总可能是20，白巧克力糖的可能是5，则相关概率是5/20=1/4，随机抽取一块糖是白巧克力糖的概率是1/4.

　　(2)已经知道抽取的糖是白色的糖，所以这可能值为12，而其中白巧克力糖的可能是5，所以，相关的概率是5/12.如果我们套用公式，P(AB)=5，(既是白色糖又是白巧克力糖的事件为5)，P(B)=12(白色糖的事件为12)，所以，P(AB)/P(B)=5/12。

　　在(2)中，事件A(抽取白巧克力糖)和事件B(抽取白色的糖)不是相互独立的事件，相反，事件A是事件B的子集。

　　对于相互独立的事件A与B，有P(AB)=P(A)P(B)。

　　这个公式的证明很简单：

　　对于独立事件A,B，有：P(A)=P(A|B)，则条件概率的计算公式可以写成：

　　P(A|B)=P(A)=P(AB)/P(B),则：P(AB)=P(A)P(B)

　　对此，可以理解为：如果两件事情是独立事件，发生与否互补干涉，则两件事同时发生的概率是每件事各自发生概率的乘积。

　　要理解这个公式，可以举一个简单的例子。比方说，你每天早上读英语诗的概率是0.4，我每天能够在7点之前醒来的概率是0.6，那么显然这两件事情是互相不干涉的独立事件。因此，某天我7点前醒来恰巧那天早上你读英语诗的概率就是这两个独立概率的乘积：0.4*0.6=0.24。

　　目前对于概率，SAT还没有做更深层次的考核，学生掌握了上面的知识和方法，就可以对考核的题目游刃有余了。