美国“高考”这门测试,最重要的数学知识点是什么?
数据分析Data Analysis
1、为什么要学会数据分析,数据分析是啥?
数学产生于人类的生产生活需要,因此数学也是用来解决生活中的问题的。这就不难理解为什么美国把数学的“应用题”叫做Problem Solving。
在比较浅显的应用题中,所有的数据信息都有其含义以及其存在的充分必要性,每一个角色都不是“路人甲”,所以读者把这些信息整合起来,就可以得到问题的答案。
然而在现实生活中,并不是所有的数据条件都非常完美,有靠谱的数据也有跑偏的杂音。因此,人们需要对数据的整体规律进行整合,从而从纷繁复杂的数据表面推知其下所蕴含的道理。例如,请看下图:
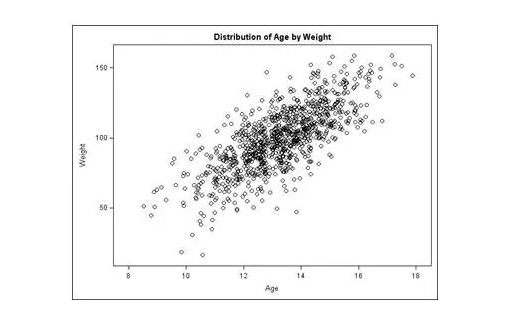
这种图形叫做scatter plot,看起来有点难看(密集恐惧症患者,我对不起你们),但是确是数据分析中常用的一种图表。这种图形是怎么绘制成功的呢?以本图而言,假设实验中我们调查了200个青少年,每个人有一组数据(年龄age,体重weight),因此每个人的数据对应坐标中的一个点。我们把这200个点都画好,就出现了上面展示的这个图形。
这个图片所关联的研究兴趣是:研究青少年的年龄与体重之间的关系。通过常识我们都可以知道:对于青少年而言,年龄越大,一定体重越沉啊。这个常识在图形中得到了佐证:age与weight之间是正向的线性相关关系(positive linear relationship)。
而且,这个图形可以告诉我们更加精确的一种关系,即:体重=slope*年龄+intercept。我们可以在这些复杂的小点点上划出一条线,这条线(y=ax+b)总结了年龄与体重之间的一个线性关系。
通过年龄,可以推知一位青少年的体重。落在这条线上或者附近的数据,可以被视为符合常规的正常数据,而与这条线距离非常远的数据(即小小年纪体重超标,或者芳龄18瘦成闪电)则被视为跑偏数据outlier。
事实上,scatter plot并非只是展现线性关系。它可以展现自变量和因变量之间的各种关系。看下面的图:
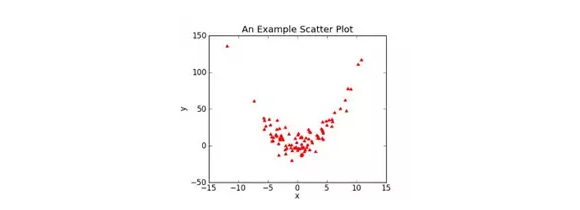
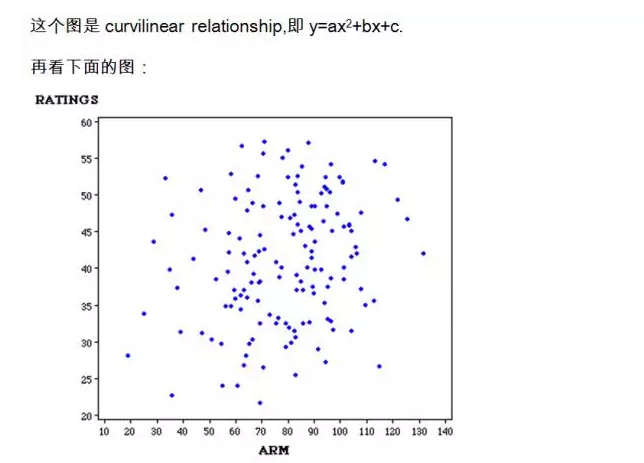
这个图自变量和因变量之间几乎没有什么关系。
综上所述,以scatterplot为例可以看出:数据分析涉及到一系列的动作。首先要通过一定的方法采集数据(Data Collection)并且记录下来。然后对采集的数据进行过滤整理,找到其背后的整体趋势,从而可以辨别数据的真伪好坏,也能对事物的未来趋势做出预测。为了总结和预测,我们采用了数据分析(Data Analysis)。
2.数据分析中经常用到的图表有哪些?
以下列出统计和数据分析中经常用到的图表。记住:具体的某个个体数字并不是非常重要,重要的是整体的趋势。对于这些图表的解释如果让学生觉得陌生,那么建议该学生跟着统计老师好好补习一下。
(1)表格Table:对于数据的详细记录。如下图所示。要求学生可以从众多的数据信息中提取自己所需要的信息,加以整理和利用。
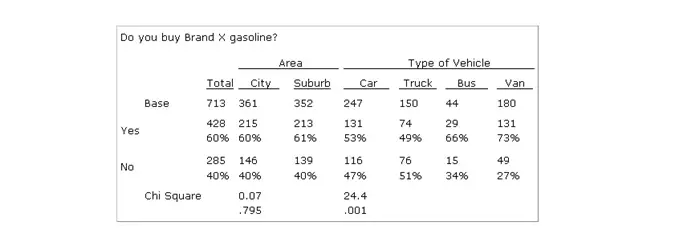
(2)柱状图Bar Graph/Histogram:看整体的趋势。如:下图是一个right skewed normal distribution。(注意:bar graph和histogram还是有区分的,但是在SAT考试中应该不会太过于区分,我也就不用细讲这个地方了。)
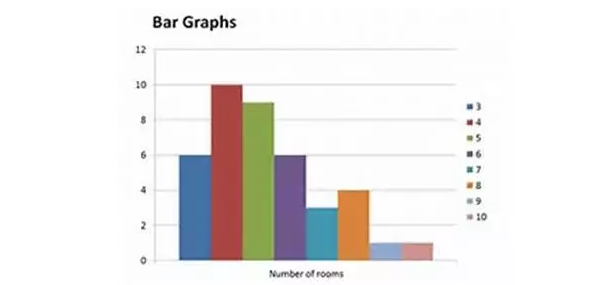
(3)线形图LineGraph.线形图表明了事物发展的总体趋势,通常而言,如果线的形状可以用某种方程来模拟,我们的数学分析就具有了预测的特征。
如下图:红线是normal distribution,蓝线是logistic regression。如果可以进一步确定这两条线各自的重要参数,就可以通过已知来推知未知。(现在想明白股市和金融市场的线形图具体是干什么用的了吧)
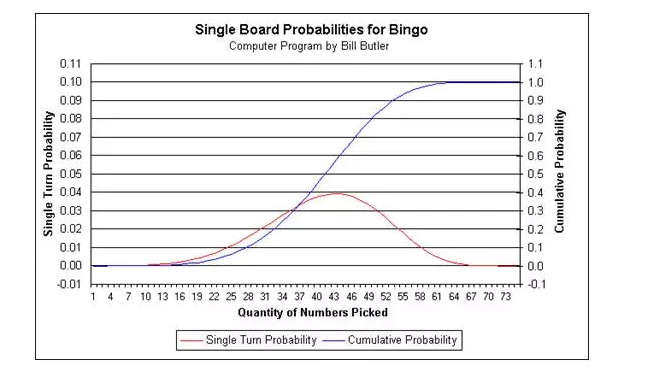
(4)饼状图piechart:主要体现的是比重proportion或者百分比percentage。大多数时候,饼状图并不体现数值,只是对于不同事物的比重进行一个比较。
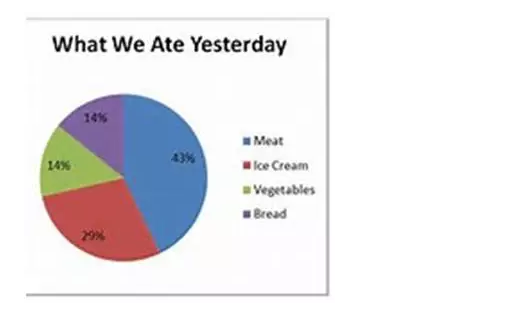
(5)Boxplot:展现数据的极值和quartiles(25 percentile,median,75 percentile),从而让人可以比较不同组数据的实质是否相同。见下图

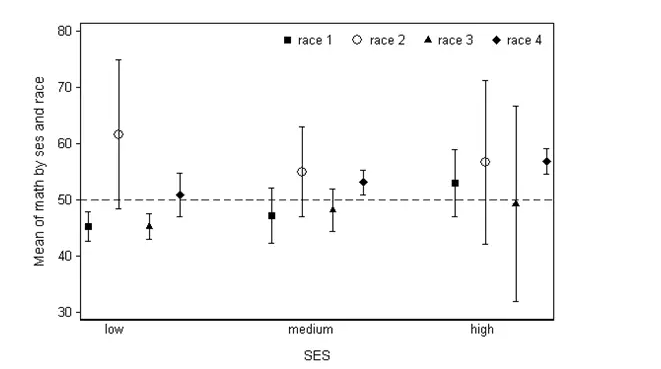
(6)Confidence Interval Graph: 展现数据的平均值mean和95% confidence interval,可以让人认出实质不同的数据组。
如下图中,组数据实质上低于第八组数据(因为组数据的高95% confidence interval还低于第八组数据的低95% confidence interval)。
在数据解释上,我们可以说:低收入家庭种族的学生明显比中等收入家庭第三种族的学生在数学表现要差。同理,我们还可以看出:对于社会中高收入的家庭而言,不同种族并不会实质性影响学生的数学表现。
3、与数据分析相关的实验experiment经常有哪些步骤?
SAT有的数据分析的题目里会涉及到一些实验的细节,对此不熟悉的同学常常会引发紧张情绪。在这里,我把实验的基本步骤简单介绍一下,作为对大家有用的知识背景。
实验的目的:通过实验来探知一个假设(hypothesis)是否正确。
实验的步骤:
(1)说明实验要验证的假设,同时要给出关键的定义以防误解。(这一步学生可以不用太多在意,因为考试的时候会在题目中把这个背景一带而过)。
(2)Literature Review(这个是把历来相关问题的文献调查一遍,一是确认自己不是重复做研究,二是找到他们所遗漏的问题,作为未来研究的方向和突破口。这一步学生也可以略过,因为我们的数学题目中不会涉及这一个环节)
(3)Experimental Design。实验设计可以有很多种方法,但是所有的方法必须要保证实验结果可以放之四海而皆准,因此,就是要保证实验个体在很多性质上都是具有代表性的。
比方说,有的实验给出男女参加人的比例或者参加人的种族(race)、民族(ethnicity)、文化背景(cultural background)、家庭经济背景(SES)、家庭文化教育背景(family educational background)等信息,其目的就是展现实验参加人对于人群的代表性。
这些与参加人有关的杂七杂八的信息叫做demographic data。这部分内容可以说的很琐碎,但是其目的就是证明代表性(representativeness)。
再比方说,实验说了用了某种方法来取样(sampling),取样的方法千奇百怪,但是其服务的目的都一样,保证所取的样本对于其所针对的目标群体(target population)具有代表性。
因此,学生们经常看到的词是随机取样(random sampling),这种取样方式是所有取样方式中最基本最常见的。
(4)Experimental Group vs. Control Group, 实验组和参照组。所谓参照组,就是不施加以实验的变量,静静地搁置在一旁的组。
他们的存在就是为了通过比较看看实验介入变量所起到的作用。比方说,要知道一种药是否能减肥,就给实验组(experimental group)吃这种药,给参照组(control group)吃长得一个样子的糖丸,然后实验期一过,通过两组的数据的对比,看看这种被实验的减肥药是否有效。
再比方说,要知道一种教学方法是否有用,就给实验组用这个方法,给参照组继续用原来的方法,实验结束后比较两组的数学提高情况。
(5)数据分析Data Analysis。这个部分是我们的重点,因为涉及到了具体的计算。题目会先说到数据采集Data Collection,这个步骤注意数据的代表性就行了,因此题目也许会说到random等关键词,通过对上文(3)的学习,学生也知道了这一点。而数据的具体分析计算才是我们的重点,是数学的真正考点。
(6)Results & Discussion。这个部分就是结果。在数学考试中,一般会让学生求出结果而不是直接给出结果,所以,这个部分我们不必过于在意。对于Discussion, 它的真正含义是说出这次实验的疏漏和不足,以期在未来得到改进。
熟悉了以上的实验步骤,就能够有效地帮助大家理解题意,顺利做题了。
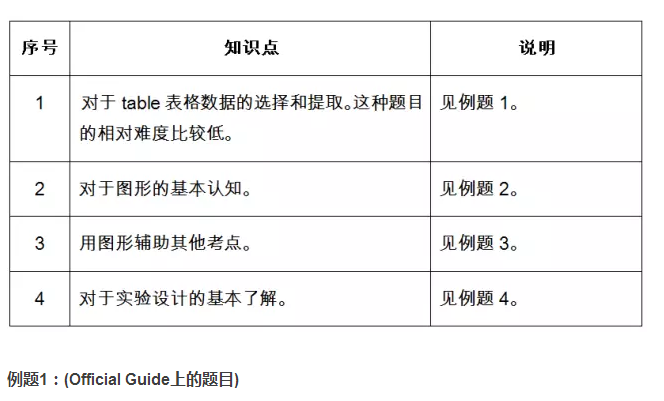
4、常考知识点与相关例题
简单说明:在这个部分,我们讲解了很多种图表的样式和用途,然而在SAT考试中,这部分的题目并没有很难,主要考核的都是基础知识。同时,也作为其他考点的辅助手段出现,目的是让学生能够学以致用,将抽象的知识运用到具体的解决问题的过程中。
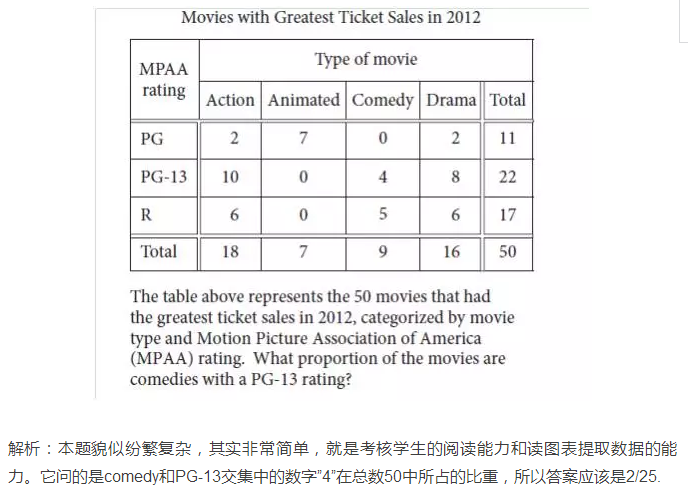
例题2:(Official Guide上的题目)
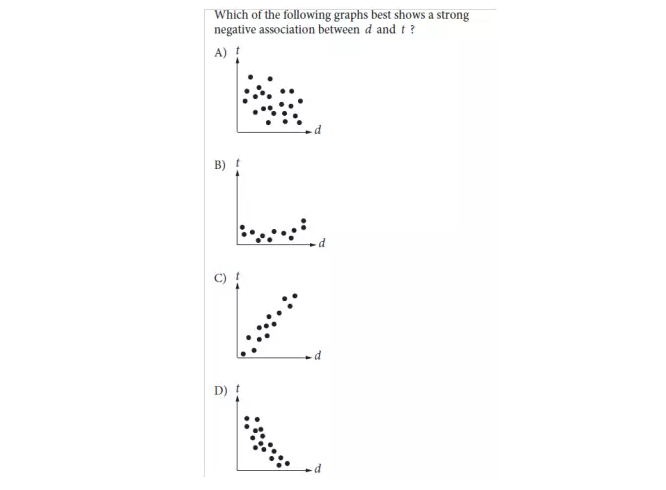
解析:这道题目问的是对scatterplot图形的基本掌握,答案应该是D。
例题3 (的Practice Test 8的题目):
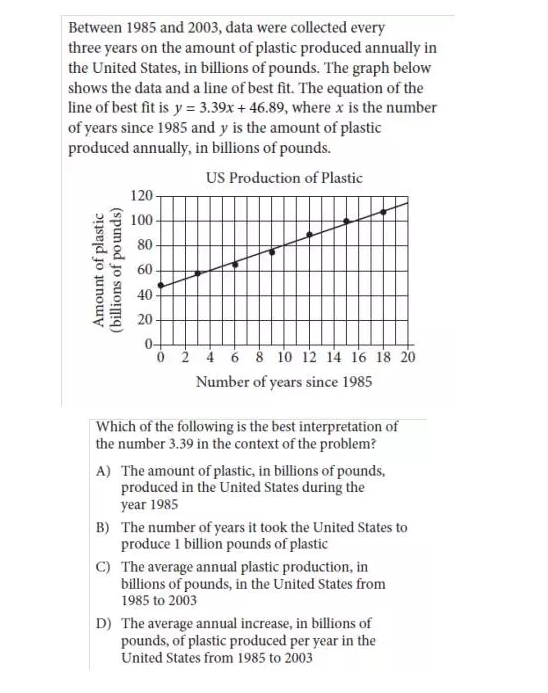
解析:这道题目以数据分析的形式出现,但是实质考察的知识是algebra里面的一元一次方程y=3.39x+46.89. 题目要求是询问slope3.39的含义。
在篇SAT数学的文章中,我曾经描述过:slope斜率意味着针对每一个单位的x的增长,y相应所作出的增长。
按照这个定义,我们发现答案应该是D,当然,这也对阅读水平提出了更高的要求。一些同学在data analysis部分丢分,本质原因不是数学能力,而且阅读水平。
例题4(的Practice Test 8的题目):

解析:本题考查的是实验设计的基本方法。如果想通过样本sample推知全体population,需要保证样本的代表性representativeness。而要保证代表性的基本方法就是random selection/ random sampling。
本题的叙述中,根本没有提及random sampling,也没有说明为什么要知道community的家庭平均孩子数目就一定要到playground去取样,因此,这个样本应该是一个biased sample。 答案选择C。









