学霸的5分AP微积分BC的备考之路！你值得拥有

今天新航道AP培训班小编请AP微积分BC5分考生来给大家分享备考心得啦!!!给正在备考的小伙伴们带来一些小方法让大家在备考中少走弯路!!!

 

微积分分为四个部分：

No Calculator Active选择题(28题，55分钟)

Calculator Active选择题(17题，50分钟),

Calculator Active Free Response(2大题，30分钟)

No Calculator Active Free Response(4大题，一小时)。

考试时间相对来说比较充裕，考生大部分情况下都能够完成题目。根据我的经验，反而是允许用计算器的部分难度会较大，陷阱会比较多，所以需要考生极其细心。

相信大多数同学认为微积分是“最简单”的一门AP;这话说的不假，但也不全对。

首先，微积分本身并非非常的简单，而是AP微积分BC的五分率非常高，可以达到接近50%。 导致其五分率奇高的原因是AP微积分BC的容错率非常高，接近25%-30%。也就是说，108分的卷子，你到了大约75分以上就可以五分了。

细心的朋友肯定发现了我这里只是特指AP微积分BC比较容易得五分，而并非AB。因为AB的五分率的确大大的低于BC。

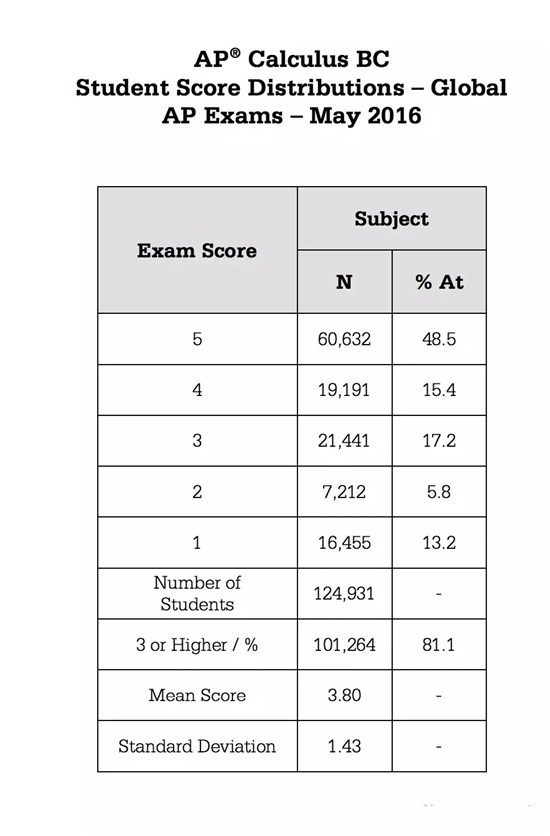
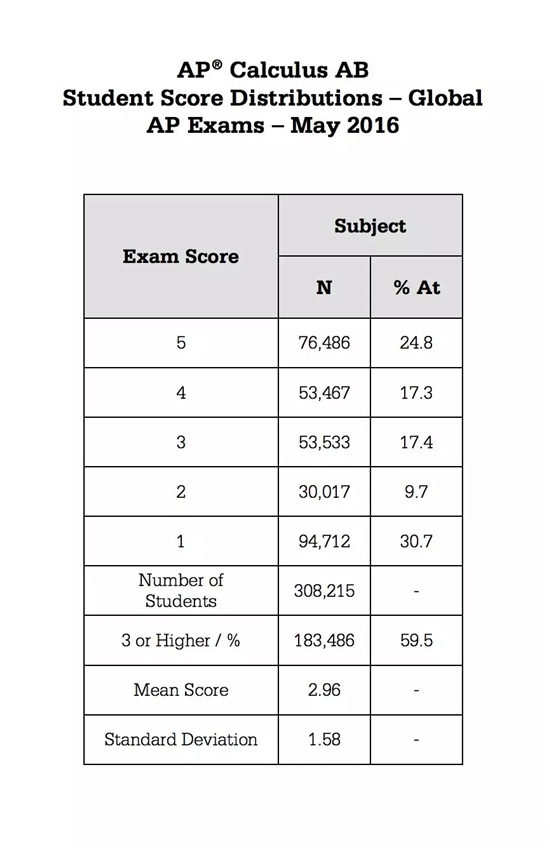
拿2016年的题目来说，微积分BC的五分率达到了48.5%，平均分数为3.8。而AB只有可怜的24.8%(但是在AP学科当中也还好啦)，其平均分数只有2.96。这并非特例，而是每年的普遍情况。

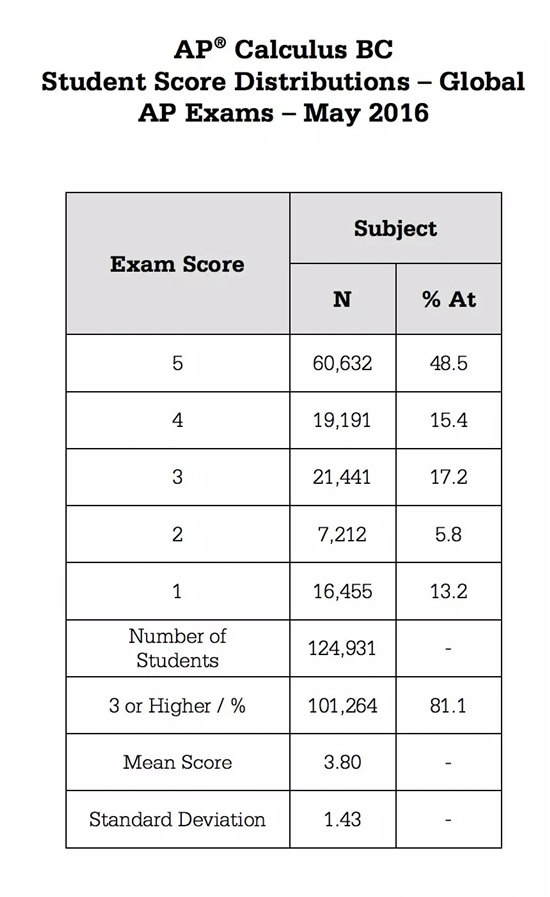
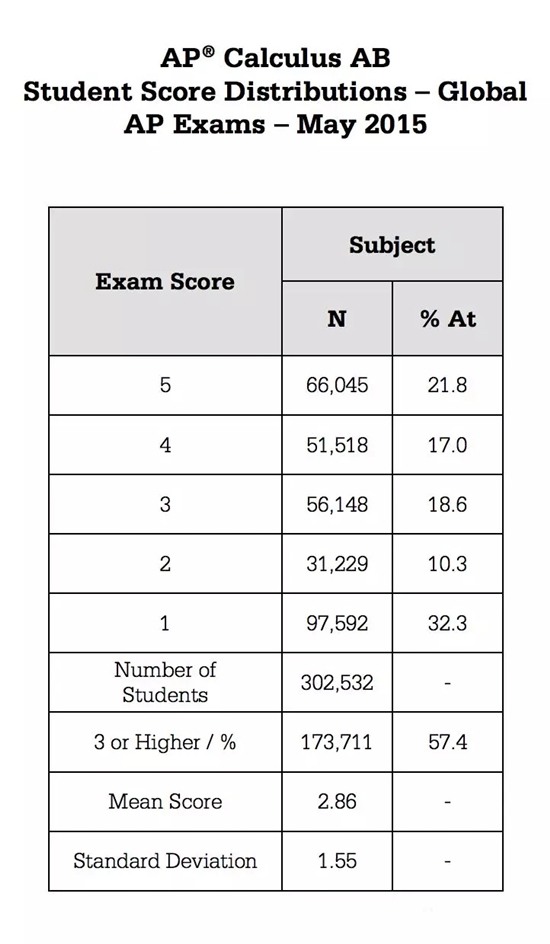
(AP Calculus 2015年全球卷分数分布。具体内容可参考CB官网)

尽管AB的五分率要大大低于BC, 并不代表AB要难于BC(当然不可能了，想想也就明白了)。导致五分率悬殊如此之大有多重原因，比如说AB的curve(可以理解为容错率)要严格于BC, 并且学BC的学生通常要更加的有准备等等。

但是从数据统计上来说，BC较于AB，要更“容易”(大误)拿五分。AB和BC并没有太大的差别，而是BC多出一章级数，其他的内容AB考的，BC也同样都考。如果还在纠结是考BC还是AB的同学，作为过来人，我还是推荐考BC的.

推荐学习教材以及相关辅助工具：

学习教材新航道小编首当其冲推荐James Steward的 Caculus: Early Transcendentals(小提琴在封面的)。

其缜密的推理以及证明让我甚至在没有帮助的情况下都能自行理解(当然老师的辅导也是必不可少的。会让你的学习效率事半功倍。)因为其实是面向大学的教材，所以它的课后习题难度会偏大，所以如果发现做题有困难的话不必气馁。

另外如果说已经系统的学过了一遍的话，推荐巴朗以及普林斯顿出版的AP Calculus来进行系统的知识点复习，在此提醒大家千万不要将这两本书作为学习微积分的入门材料，因为其书中的内容只是简单的将知识点进行了整理方便大家温故，而不是作为理解微积分的材料。

两本书各有优缺点，普林斯顿题目过于简单，没有任何借鉴价值;巴朗的题目要难于AP，所以在时间允许的情况下有一定的刷题价值，当然其题目套路和AP有一定的出入，所以了解题目的方法还是做真题本身。College Board官网上有历年的Free Respons题目，也就是后两部分的大题。

而前面的选择题部分只有1969-1998其中一些年份的集锦，相比于Free Respons要稀缺不少，而且题目的参考价值也没有2000年之后的要高。而在CB官网是找不到2000年之后的题目的，网上能找到的题目也很不完全，所以的方法就是问尚学名德的老师，其题目数量会满足你拿高分的欲望的(做个广告嘻嘻)

另外，Khan Academy和Slader.com是课下自学的学习网站(美高的同学懂我在说什么)。Khan Academy上有非常系统的AP微积分讲解，涵盖大大小小的细节知识点，作为课下的辅助参考非常有用。Slader.com上能搜到很多教科书的题目的回答，以James Steward这本书为例，基本上每一章节背后的题目都会有各种大神的解释，所以作为做题时候的参考也是非常有帮助的。

计算器的选择也是非常重要的，或者说一个好的计算器会直接的影响到你的学习效率以及考试状态和做题速度。相信Ti-84是大多数人的入门Graphing Caculator(如下图)。

虽然其功能强大，但是操作简陋而且繁琐。在考试当中会浪费大量时间;比如输入一个积分符号或者值符号都会在操作界面上选择半天，因而会直接影响到考试的速度。

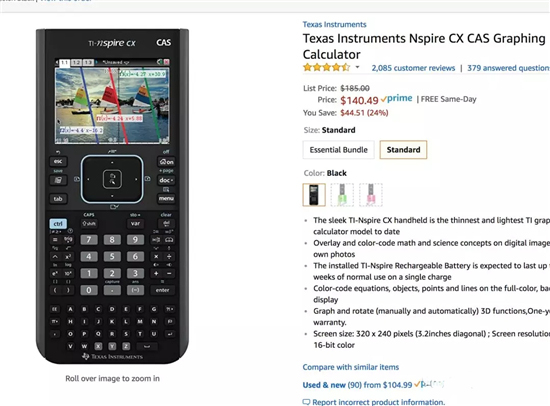
所以我一般都推荐购买Ti-Nspire CAS, 功能更加的强大，并且操作更加的简单;操作界面更加的明了;最重要的是它可以解不定积分，在关键时刻可以省掉用各种techniques来解不定积分的时间。就是价格稍微高一点，但是40刀左右的差距也比较合理。所以在条件允许的情况下，我极力推荐Ti-Nspire CAS.

备考过程：

我是从去年暑假开始接触AP微积分的。我本身数学不是特别突出，并且所在的学校也是一个较注重文科的学校，所以在理科的学习上并没有很大的优势(应该说是的弱势)。因此，我在学习Calculus上算是起步比较晚的。

微积分说难，它也很简单。说简单，它也不容易。难是难在它琐碎的知识点，如果单纯靠死记硬背会比较痛苦，所以这也是为什么很多同学会抱怨学习微积分很痛苦。但是其实在我看来，只要正确理解微积分的基本思想，就能够循序渐进的沿着一条主线理解。

所以在最初的学习准备中，理解微积分的“基本思想”——极限——是最重要的，也是直接通往微分积分世界的“葵花宝典”。其实微积分思想也会经常体现在我们小学以初中的数学学习过程中，比如在我们小学学习计算圆面积时，老师们教过我们把把圆像西瓜切成多个小的齿状，然后拼成一个长方形，用长方形公式计算。

当然，这里永远有误差，而且误差的多少是建立在我们切的齿状扇形的数量。齿状越多，面积计算就越精确，误差也就最小。所以如果我们把圆切成无限个齿状就可以的求出圆的面积了呢?是的。但是“无限”这个概念非常虚，因为我们永远知道“无穷远”是多远，所以我们就需要一套理论来“定义”它。极限(limits)是微积分的“公理”，就像“两点之间距离最短一样”是几何学的公理一样。

正确的理解极限的意义以及求极限的方法是微积分的入门，也是掌握微积分思想最重要的一步。理解极限以后，求导数(Derivative) 也会迎刃而解，无非是将求极限的方法带入到了计算方程的斜率当中。同理积分(Integral)，可以理解为求导的逆运算。级数一样，虽然和微分积分看上去略有不同，但是也是利用极限思想来探索级数的收敛以及发散。

所以了解了极限的意义，方能够理解微积分的“升维降维” ，及求导数和积分(differentiate and integrate)，以及微积分的应用，比如位置、速度加速度、人口增长速率、面积体积等等;甚至连这两年占据各大新闻版面的“人工智能”本质上也用到了微积分的方法，其令人惊叹的“机器深度学习”能力背后都有一个深层而又复杂的神经网络，而这个网络就是一个错综复杂的函数，里面有上亿个待训练的参数，而训练参数的方法本质上也是利用“梯度下降法”(Gradient Descent Optimization)来进行无数次的迭代，其实也是利用了微积分的“升维降维”的思想。

说了那么多，无非是想告诉大家不要死记硬背，而是逐步理解微积分背后的奥妙。

微积分知识点很多，难点也不少，而且每个人认为的难点也各有不同。根据我的经验，在微分这一章节里面，大部分人都会在微分应用这里稍微卡一点。因为各种在现实生活中的应用可能比较抽象，比如“瞬时速率”(Instanteous rate of change)以及其牵扯到的“相关变率”(Related Rate)和“化”(Optimization)问题确实会让人一开始有些摸不出来头脑。

但是只要多做题目就会发现大多部分的题目做法非常的相似：只要找到各个变量和常量间的关系，用基本的求导就能解决大多数问题。其难度的增加无非是变量和常量的增加从而对理解造成的迷惑性，以及各常量和变量构成函数的不同。从积分开始计算就变的越发复杂，所以需要大家尤为的心细以及认真。在我看来，积分的难点基本上都在解不定积分以及体积的计算那里。

不定积分的解开有众多的方法，所以需要各位熟练掌握每一种方法，并且的判断应用于某一个函数的方法(也有可能是多个方法的杂糅)。很多人对我反映级数(Series)这一章节难度较大，但是我持有中立的态度，因为我觉得并非和之前学的内容有过大的难度差异。

总结下来，认为大多数人都是在考试前匆匆忙忙带过这一章节，因此学习的时间较短，而且最后大家心情会普遍浮躁一些，所以可能会导致普遍认为级数较“难”的错觉;不过在我看来，反倒这一章节相对要更简单，因为其涉及逻辑以及理解的内容却更加的少。

大多常考的题目无非是利用各种判别方法 来判断一个series是否收敛(Convergent)或者发散(Divergent)，以及计算其收敛半径，但是因为繁多的判别方法所以可能一开始会有些晕头转向。但是好在AP微积分不会考判别方法的推到过程，所以不需要对于判别方法有深层次的理解，而是像工具一样会用就行。

还是那句话，“我亦无他，惟手熟尔”，只要多练习，就能够熟练的在短时间内判断出求级数极限状态的判别式，从而判断其是否是收敛或者发散。所以这一部分最简单的方法就是在了解基本辨别式所对应级数的常见形式，然后加以练习。

在此上海新航道小编建议大家不要纠结于某个级数收敛发散的原因，因为很多级数的发散收敛情况很难想象出来。就像大多数人一开始很难理解调和级数为什么是发散，确实 ，1/2+1/3+1/4…∞ 是一个收敛的数列，所以大多数人次都会误会它是一个收敛的级数，然而用简单的证明就会发现其实并不是.在此要提醒大家，数列收敛不代表级数收敛，

但是级数收敛其数列必定收敛，不要纠结判别式的推导过程，AP不考所以会用就好。然后就是泰勒级数(Taylor Series)，也是我自认为掌握的最不扎实的一部分。其实泰勒级数的理解并不是非常复杂，就是在某个函数的一个点作一个多项式，通过局部近似的方法无限增加这个多项式的order，让此多项式的每一个点以及其导数与原函数重叠。

其本质是想用一个幂级数展开式来表达一个f(x)函数。泰勒级数的公式相比于之前学过的公式较为复杂，不过记忆的话也是有迹可循的。因为其公式较为复杂的原因，所以与它相关的应用题目也会比较复杂。

所以需要清楚的记忆泰勒展开式以及其发展的规律;另外，一定一定要记住常出现的Maclaurin Series(当Taylor Series的中心点位于x=0点时的特殊形式)，比如 1/(1-x), e^x,sinx, cosx, ln(1+x),tan-1x等等，关键时刻能够省去很多泰勒展开的时间。

最后就是最恶心的“泰勒余项”了，或“拉格朗日余项”(Langrage Error bound).这个解释起来非常麻烦，不过可以确定的事考的不多，一般2年会有一题，而基本上都是在选择或者大题的最后一题，所以记住公式会用就好。每个人认为的难点都不一样，一一罗列也不太现实，所以以上只是鄙人认为相对头疼点的点。

关于复习备考，我犯了很大的错误就是没有提前刷题，而是在考试提前两周时间内才大量的刷题目，所以在学校课程还在进行的同时显得有些仓促。

AP微积分的知识点分布比较均匀，基本上所有的知识点都会有考到，这既是一件好事又是坏事;好的是因为其知识点分布均匀所以我们不会因为某个知识点的不熟悉而导致大部分失分，所以考试的结果都会比较稳定客观;坏的是需要我们将每一个小的琐碎的知识点都复习并且搞懂，就算再“久远”(在章学到的等等)的知识点，都有很大的可能会被考到。

当然，对于准备充分的同学就没有这方面的疑虑。所以我建议将近20年来的题目(其实没有很多啦，不是每年都有)都系统的做一遍，在每做一套做的同时记录下自己不熟悉的知识点，然后加以复习。做了两三套以后就会发现质的飞跃。另外，千万千万不要抱着“虽然这个知识点不熟悉，但是反正也就一份啦无所谓”的心态。尽管AP微积分的容错率高的变态，但是多错几道5分也就跟你说拜拜了。。。所以大家还是要复习透彻，把再小的细节都搞清楚。

 

上海AP课程哪里好?新航道上海AP课程培训中心开设有AP物理1&2课程培训、AP电磁学课程辅导、AP力学辅导等等，上新航道跟学霸为伍！