2017-03-28 09:14来源:互联网作者:上海管理员
摘要:这篇文章是新航道英语整理的AP微积分知识点梳理。
AP马上就要考试了~小伙伴,你们还好么?
这篇文章是新航道英语整理的AP微积分知识点梳理。公式大全,请:2017AP微积分公式大全(下)、2017AP微积分公式大全(上)

微积分考试分为AB与BC,与AB相比,BC包含的内容更多、难度更高。考点包括极限、微分、积分(不定积分、定积分)、微分方程、级数(AB无此部分)、应用。
1极限部分
这部分是微积分的基础,包含:
(1)会判断极限存在或不存在,当极限存在时,如何求出该极限
(2)利用极限刻画函数的形态——渐近线(asymptote),研究函数的性质——连续性(continuous)。
1.1 极限存在的判定标准:左极限与右极限均存在且相等
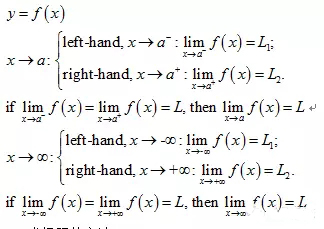
1.2 求极限的方法
求a:先将a代入表达式,如果可以求出某一确定的数值,则该数值即为此函数的极限。
1.2.1 有理函数(rational function)
一般来说都是0/0或infinity/ infinity的形式,
求a:通过因式分解将0因子约掉。
求无穷大(infinity):分子分母同时除以该式子的次项。
另外也可用L’Hopital’sRule来做。
1.2.2 洛必达法则(L’Hopital’s Rule)
具体使用时,如果所求极限是0/0或infinity/ infinity的形式,可以将分子分母两部分分别求导,再计算求完导数之后的极限。
1.2.3 等价无穷小代换
这一方法大部分国外教材与辅导书(James,Thomas,Finney,Barron)都未提及,但掌握之后会给运算带来相当大的便利。
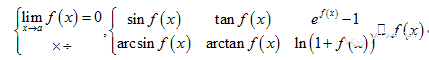
1.2.4 幂指函数
即
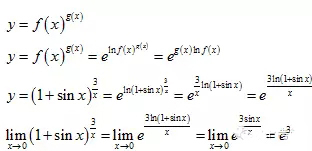
这种类型的函数,做法是通过ln将其变换成指数型函数来进行运算。
1.2.5
0乘有界等于0
1.3 对于极限不存在,需要掌握左右极限不相等、无穷大和震荡三种
1.4 极限的应用
1.4.1 函数的连续性(continuity)
如果函数在某一点的极限值等于函数值,则称该函数在这一点连续。判断函数在某一点是否连续,必须要分别考察其左极限与右极限,如果左极限与右极限相等则说明极限存在,进而与该点的函数值比较,如果相等即为连续,不等即为间断。
1.4.2 间断点的类型(discontinuity)
一共分为三种removable,jump,infinite
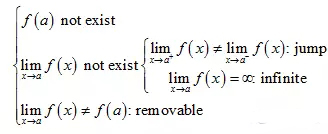
1.4.3 当函数在某一闭区间上连续时,则有三个定理
(1) The extremevalue theorem (EVT)
(2) Theintermediate value theorem (IVT)
(3) The zeropoint theorem (Bolzano theorem)
1.4.4 渐近线(asymptote)
分为水平(horizontal)与垂直(vertical)。
其中水平的求法是分别求两个infinity的极限,如果存在则可判定有水平渐近线。
垂直的求法是求某一点的极限,如果该极限等于无穷(infinity),则可判定通过在这一点存在垂直渐近线。
水平(horizontal):
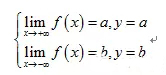
垂直(vertical):
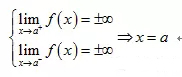
2导数与微分
这一部分的核心在于如何求出一个函数的导数及导数的应用。2.1 导数与微分的定义
简单来说,导数是切线的斜率(slope),微分是切线的改变量。
2.2 求函数不同表示形式的导数
显函数,反函数,复合函数,隐函数,参数方程,极坐标
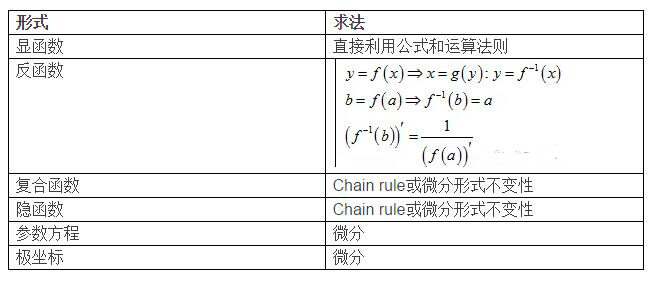
2.2 高阶导数 要注意的一点以哪个变量为基准求导数,默认是x,但也有特殊情况,如respectto sinx,则是将sinx看成一个整体进行求解。
它是在导数的基础之上再求一次导数,常用的是二阶导数(second derivative)
2.3 导数的直接应用
导数的直接应用是求切线和法线。
求切线的时候需要注意的是所给的点是否在已知曲线上,如果在则可直接求导代数求出切线斜率(slope),如果不在则需要先设出切点,而后通过解方程的形式把切点和斜率解出来,从而得出切线。
2.4 可导与连续
在某一点可导必然连续,而连续则不一定可导。
2.5 中值定理(mean value theorem)
从几何图形上来看,当函数在闭区间上连续、开区间内可导时,必然存在一点c使得过c点切线的斜率等于端点连线的斜率。
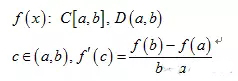
利用中值定理可以对函数进行估值和给导数估值。
3导数与微分的应用
3.1 函数与导数的关系
函数的增减性可由一阶导数的正负来判断,凹凸性可由二阶导数的正负来判断。
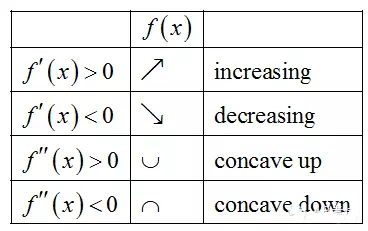
3.2 驻点与拐点(critical and inflection point)
不同的教材对这两个点的定义不同,我们这里采用比较通用的
3.3 求函数在某一闭区间上的max and min
极值(local/relativemaximum and minimum):邻域内或最小
最值(global/absolutemaximum and minimum):整个区间内或最小
对local来说,步骤如下:
(1)求出一阶导数等于0和不存在的点
(2)利用一阶导数是否改变符号和二阶导数的正负来判定。
对global来说,步骤如下:
(1)求出一阶导数等于0和不存在的点
(2)求出所有的函数值,的即为global max,最小的即为global min。
3.4 物理应用:运动
运动分为直线运动与平面运动,最原始变量为位置函数,由位置函数来定义位移(displacement)和路程(distance),在位移(displacement)的基础上定义速度(velocity)和速率(speed),在速度的基础上定义加速度(acceleration)。
平面运动的位置函数用向量(vector)来表示,因此后面所有的变量都是向量的形式。
直线运动的主要问题
(1)求加速与减速区间
(2)求在哪一时刻改变运动的方向
(3)求某一时间段内的路程(distance)
平面运动的主要问题
(1)速度向量、速率和加速度向量
(2)求某一时间段内的位移(displacement)和路程(distance)
3.5 相关变化率
这一部分是应用题,现实生活中的某一个量随时间变化而变化,进而求:
(1)某一时刻该量的瞬时变化率
(2)某一时间段内平均变化率
(3)某一时间段内的累积量(积分的应用)
4不定积分和定积分
4.1
与导数类似,不定积分这一部分主要是它的求法,基本的积分公式与运算必须非常熟练。
(1)换元法(substitution):将被积函数的某一部分用另外的变量代替,从而将被积函数化简,使用积分基本公式得出结果。
(2)分部积分法(integral by parts):适用于求两类不同函数乘积的积分,核心是通过交换来改变被积函数,从而将难求的变成容易求的。
(3)有理函数积分:对于分母是1次和2次的形式有固定的套路,掌握即可。
4.2 定积分
1.黎曼和(Riemann sum)
使用近似逼近的方式来求面积,常用的是左端点、右端点、中点、梯形来做估计,步骤如下
(1)将区间等分成n份(也可不等分)
(2)按照预先设定的规则求出每一部分的面积
(3)加总。
利用黎曼和对定积分或面积进行估值,需要比较估计值和真实值的大小,可比较的是左端点、右端点和梯形三种估计方法,中点由于大小不易确定,较少出现。
黎曼积分则是在加总之后求极限,那么该极限值应该等于图形面积的真实值,也就是定积分的值(黎曼可积)。
2.求定积分的基本方法
牛顿-莱布尼茨公式,使用该公式时先求不定积分,再代入数值,因此不定积分的方法都可以在这里使用。但是需要注意的是,使用换元法的时候,变量的取值范围会发生变化。
3.求定积分的特殊方法
(1)对于某些规则图形(三角形、圆等)可用其几何意义直接算出面积,再利用定积分和面积之间的关系来求
(2)利用奇函数和偶函数的性质来求。
4.积分中值定理
求函数在某一个区间上的平均值或积分中值,使用如下公式即可。
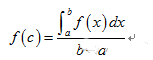
5.变限积分
当被积函数确定时,积分值会随着积分区间的变化而变化,因此可将积分值看做积分区间的函数,其中需要掌握的是变限积分的求导。
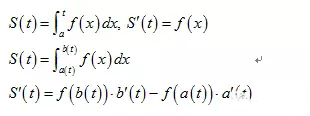
6.反常积分(improper integral)
当积分区间不是有限区间(即包含无穷大)或积分区间会使被积函数为无界的时候,求积分需要用到极限,如果极限存在,则称积分收敛(converge),不存在则称为发散(diverge)。
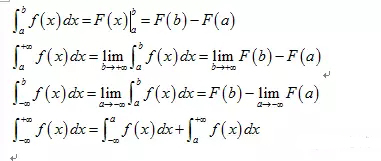
5定积分的应用
求面积、体积、弧长
5.1 面积
求平面曲线围成的平面图形的面积,一般来说是给定一条或若干条曲线,求它与x轴、y轴或其他直线或曲线围成图形的面积。
对于直角坐标系,使用定积分的几何意义来求,但需要注意的是面积永远是正数,而积分值有正有负,因此当函数大小关系或区间的边界发生变化时,要注意区别对待。
5.2 极坐标求面积
面积公式与直角坐标不同,特别需要注意的是积分的范围,如果不好判断,可用半径来反求角的范围。
5.3 体积:
求平行截面面积已知的立体图形的体积和旋转体体积,种图形对截面面积求积分可得体积,第二种图形有两种求法,种也是对截面面积求积分,不过要注意旋转截面是实心圆还是圆环,第二种是利用shell来求,掌握好展开后的圆柱壳的长宽高即可。
5.3 弧长
弧长公式用四种,一般来说在考试中如果是不允许使用计算器的部分,只会要求考生列出计算公式,不要求算出数值,而允许使用计算器的部分则可利用计算器来计算弧长的数值。
6微分方程
6.1 解微分方程:
对变量可分离的微分方程,解法是将x和y分离后,等式两边同时求积分。
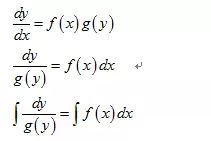
6.2 斜率场(slope field)
根据微分方程原函数每一点切线斜率计算出来,而后将与该点切线斜率相同的线段画在坐标系中,由此所形成的图形即为斜率场。斜率场所描绘出的图形即为微分方程的解。
6.3 增长模型
分为三种:
指数型增长(exponentialgrowth)
有限制的增长(restrictedgrowth)
逻辑斯蒂增长(logisticgrowth)

6.4 欧拉估值(Euler’s method)
多次使用中值定理进行估值,此时c不再任取,而是固定取每一步的起始值。
7级数(series)
级数共分为三部分:
无穷级数(infiniteseries)、幂级数(powerseries)、泰勒级数(Taylorseries)。
7.1 无穷级数
分为正项级数(positive)、交错级数(alternating)。
这部分的核心是如何判断一个级数是收敛(converge)还是发散(diverge)。
1 正项级数(positive)
判别法有三类五种,分别是积分(integral)、比值与根值(ratio and root)、比较及极限(comparison and limit comparison)。
2 交错级数(alternating)
莱布尼茨准则(Leibniz)
收敛(converge)分为收敛(absolute converge)和条件收敛(conditional converge)。
3 判定顺序
(1)将级数加值取正
(2)对通项求极限,若极限不等于0,则可判定为发散,若等于0,则(2.1)利用积分(integral)、比值与根值(ratio and root)、比较及极限(comparison and limit comparison)判定,若收敛,则原级数收敛,若发散,则(2.1.1)若原级数为交错级数,利用莱布尼茨准则判断,若收敛,则为条件收敛,否则为发散。
7.2 幂级数
利用比值法求出收敛半径(radius of convergence)和收敛区间(收敛域)(interval of convergence)。
幂级数的性质:
幂级数在收敛区间内(1)连续(2)可微(3)可积。
7.3 泰勒级数
(1)将函数展开为泰勒级数
(2)求泰勒级数的和函数。
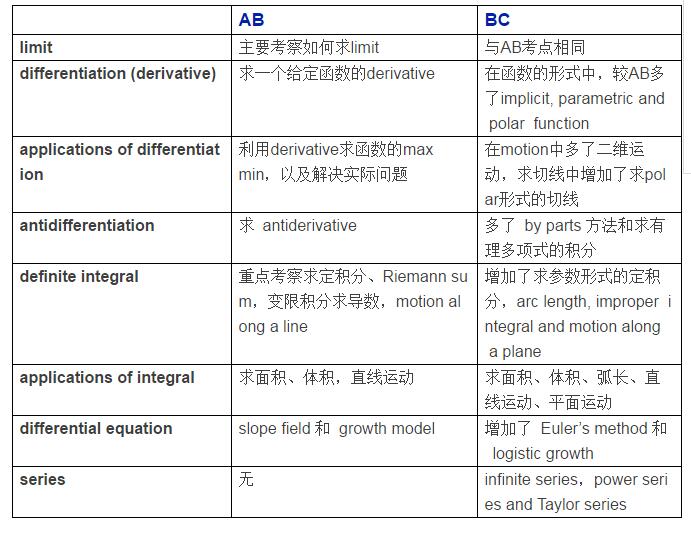
AB与BC考点对比
新航道上海AP课程培训 中心,是新航道集团和美国Kaplan教育集团共建设,美国大学理事会在中国授权的AP嵌入式课程学习中心,AP Code:694387。
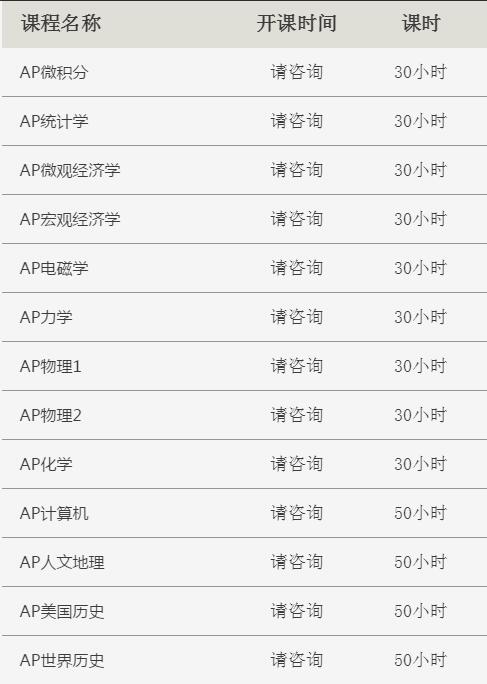
我们开设有多重AP课程,感兴趣的同学还可以在线咨询哦!
免费领取最新剑桥雅思、TPO、SAT真题、百人留学备考群,名师答疑,助教监督,分享最新资讯,领取独家资料。
方法1:扫码添加新航道老师

微信号:shnc_2018
方法2:留下表单信息,老师会及时与您联系
| 课程名称 | 班级人数 | 课时 | 学费 | 报名 |
|---|---|---|---|---|
| AP宏观/微观经济学 | 3-6人 | 40课时 | ¥11800元 | 在线咨询 |
| AP微积分 | 3-6人 | 40课时 | ¥11800 | 在线咨询 |
| AP统计学 | 3-6人 | 40课时 | ¥11800 | 在线咨询 |
| AP计算机原理 | 3-6人 | 40课时 | ¥11800 | 在线咨询 |
| AP化学 | 3-6人 | 40课时 | ¥11800 | 在线咨询 |
| 课程名称 | 班级人数 | 课时 | 学费 | 报名 |
|---|---|---|---|---|
| AP物理1培训班 | 3-6人 | 32课时 | ¥11800 | 在线咨询 |
| AP物理2培训班 | 3-6人 | 32 | ¥11800 | 在线咨询 |
| 课程名称 | 班级人数 | 课时 | 学费 | 报名 |
|---|---|---|---|---|
| AP美国历史 | 3-6人 | 80课时 | ¥22800 | 在线咨询 |
| AP世界历史 | 3-6人 | 60课时 | ¥22800 | 在线咨询 |
| 课程名称 | 班级人数 | 课时 | 学费 | 报名 |
|---|---|---|---|---|
| AP一对一 | 1人 | 按需定制 | ¥ | 在线咨询 |
免责声明
1、如转载本网原创文章,请表明出处;
2、本网转载媒体稿件旨在传播更多有益信息,并不代表同意该观点,本网不承担稿件侵权行为的连带责任;
3、如本网转载稿、资料分享涉及版权等问题,请作者见稿后速与新航道联系(电话:021-64380066),我们会第一时间删除。
客服热线电话:400-8125888
总部:北京新航道教育文化发展有限责任公司
总部地址:北京市海淀区中关村大街28-1号6层601 集团客服电话:400-097-9266
Copyright © www.xhd.cn All Rights Reserved 京ICP备05069206
ICP认证:京ICP备05069206号-5
![]() 京公网安备11010802021513号
京公网安备11010802021513号