做不对SAT数学中的几何题，你还需梳理相关知识点！

　　做不对SAT数学中的几何题，你还需梳理相关知识点！这类题目与代数类题目相同，学生遇到的个难点是数学相关词汇，如：勾股定理的英文叫做PythagoreanTheorem。考生如果不熟悉这个词组，就会遗漏一个重要的解题条件。同样，对于题目的数学表述也是学生必须掌握的阅读能力，否则，做题的正确率要大打折扣。

　　1三角形Triangle

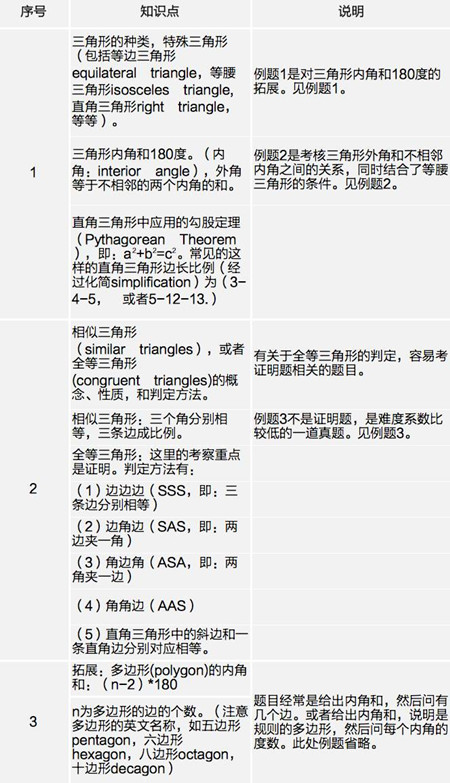
　　例题1：(2016年11月的亚太题目)。真题下载，请：完整版2016年11月5日亚太SAT真题PDF版下载

　　解析：本题实质上是等腰三角形求内角度数的拓展。将MP连接起来，可以得到MNP和MQP两个等腰三角形，因此角NMP的度数是(180-28)/2=76度，角QMP的度数是(180-100)/2=40度。因此，角M的度数为116度。

　　句话给出的是题目的实际含义和背景。本题的考点是对于一元一次方程的解释。对于本题的阅读感到吃力的同学，请努力提高数学的阅读理解水平。

　　例题2：(2016年10月的北美题目)。真题下载，请：2016年10月1日北美SAT真题

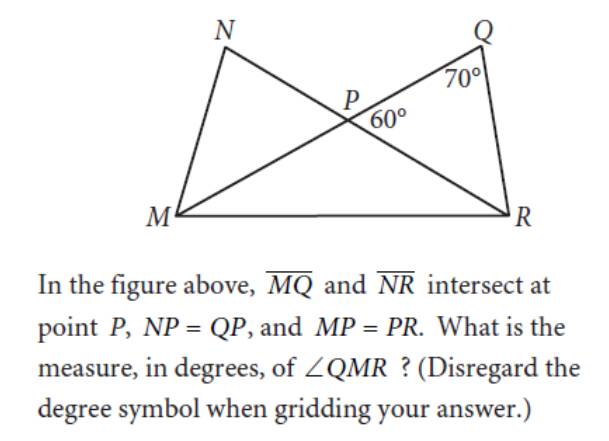
　　解析：这道题目的很多条件其实并不需要充分利用。在线段MQ上，外角QPR等于不相邻的两个内角(QMR和NRM)之和。与此同时因为MP=PR知道三角形PMR是等腰三角形，且QMR和NRM度数相等，均为30度。因此得到了题目的答案。

　　至于说，三角形MNR和MQR是全等三角形，或者三角形MPN和RPQ是全等三角形，这样的条件并不需要用到。不必过分推导。

　　例题3：(2016年5月的亚太题目)。真题下载，请：2016年5月亚太地区完整版新SAT真题下载

　　解析：这道题目的求解运用到了特殊三角形(3-4-5型号的直角三角形)和相似三角形。由三角形BCD的直角和两条直角边6,8可以知道线段CD长度为10。由AE是BD的三倍可以知道：CE也是CD的三倍，所以CE的长度应该是30。

　　2圆Circle

　　知识点

　　例题4：(2016年5月的亚太题目)

　　解析：本题非常简单，只需要学生知道圆周角是360度即可。100/360=5/18，即为答案。本题是以角度制作为计算基础的题目，比较简单。

　　圆的内接三角形的性质：

　　三角形的一个角(叫做圆周角)等于与它共享同一段弧的圆心角的度数的一半。

　　若该内接三角形的一条边是圆直径，则该三角形一定是直角三角形，该直径边是斜边。(从外切圆的角度，这句话可以说成：直角三角形的外切圆的圆心，是该直角三角形的斜边的中点。)

　　圆的内接四边形的性质：

　　圆内接四边形的对角互补，即：对角和为180度。

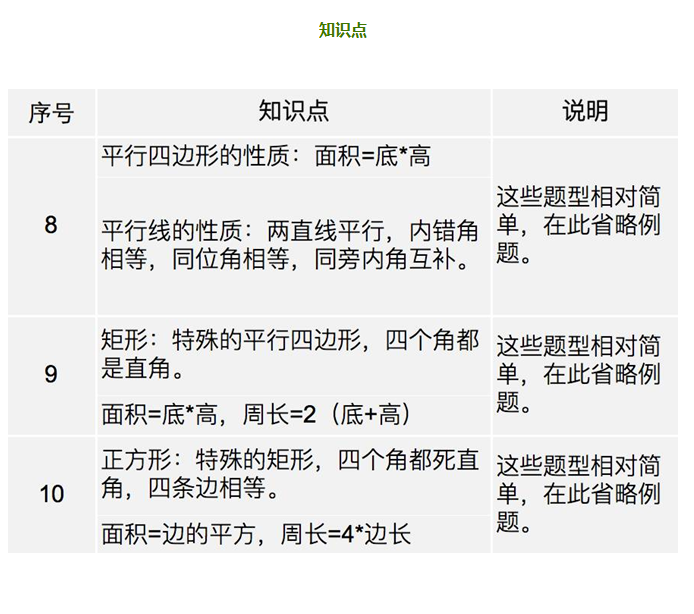
　　3平行四边形Parallelism/矩形Rectangle/正方形Square

　　如图所示：圆O是等腰梯形ABCD的内切圆，切点分别为EFHG。已知：AB=4cm,圆的半径=3cm。求：AD的长度

　　解析：目前的SAT数学还没有考到这个难度，但是学生们不妨现在开始准备起来，以防万一。本题我给出的解法并非解法，仅供参考。

　　因为AB=4，则AE=2(因为三角形AEO与BEO全等，顾AE=EB=2);

　　因为三角形AFO和AEO全等(角边边)，则AF=AE=2.;

　　同理，三角形OFD和OGD也全等，因此知道FD=DG。

　　在这两套全等三角形中可以知道，角EAO=角FAO，角FDO=角GDO。因为角A+角D=180度，所以知道：角FAO+角FDO=90度，即：DO垂直于AO。因此知道：AD*FO=DO*AO;

　　AD=2+FD，FO=3,DO=(FD的平方+3的平方)的平方根，AO=(2*2+3*3)的平方根;

　　因版面所限，我这里给出的并不是正规的数学表达式，而是其描述性表达。希望学生能够理解。

　　同时应该注意的是，很多学生会错在最后一步，往往是求出x=4.5就以为万事大吉，而忽略了题目的要求是求出AD的长度。

　　有的时候，题目是把一些基础的形状做以整合。

　　例题12：如下所示：(2016年11月亚太题目)

　　解析：本题是将直角三角形和正方形联合来考核。

　　由2AC=3AB可知，AC/AB=3/2。可以假设AC=3，AB=2，正方形的边长为x.通过证明可知：三角形BFE,EDC是相似三角形，因此BF/FE=ED/DC,即：(2-x)/x=x/(3-x)。由计算可知：x=6/5。阴影正方形的面积为36/25，这个面积是三角形面积3的12/25。选择D。

　　新SAT中对于体积一般都给出公式，可见并不十分强求学生能够背出公式。然而，它会考到不同形状的组合形状的体积，看看学生是否能够灵活掌握。见如下例题14(Official Guide上面的题目)：

　　解析：这个silo由三部分组成，一个圆柱(25π*10)和两个圆锥(2*(1/3)*25π*5)。因此，这个体积大致为1000多一点，应该选择答案D。本题并不难，难的是比这个还要复杂的图形，但是基本原理是一样的。

　　本文主要总结了新SAT在几何部分会考到的题目的要点和特征。有关于其他的考点和相关特征，将会在之前和后续的文章中继续总结。希望对于广大考生有所助益。

　　这个暑期，来新航道SAT培训班 ，我们给考生的保障

　　签订协议，承诺不过重修，只有的SAT培训学校，才敢做出如此承诺!

　　自信，源于上海新航道完善的SAT培训体系

　　13年来，我们专心做好一件事

　　那就是如何让学员顺利通过SAT考试