碰到不会的SAT数学真题该怎么办？

多年来一直在努力攻克SAT数学题;已经在课堂上学过大部分的公式;阶段测试前总是熬夜准备;并且可能也学到了很多解决代数和几何问题的快捷方式。但有个不争的事实——除非你是数学天才，否则你总会碰上你很难解开的SAT数学题。即使这样还是有值得令人欣慰的事实——当你遇到很难的SAT数学题时，基本上总有那么一两个技巧可以更接近正确答案。

当然，您采用的具体策略取决于您所面临的问题类型。SAT数学题有三个主要题型：代数核心分析，问题解决和数据分析，以及数学进阶。每一个题型都有让学生犯难的题目。接下来上海新航道SAT培训小编就带大家了解一些在不会解题时应该怎么办的小诀窍!

拿下代数核心分析题

到目前为止，代数核心分析是SAT数学题中最常见的题型，代数核心分析题涉及线性方程、方程组、线性不等式和不等式组，偶尔也会抛出一两个值的题目。

也想刚开始你会觉得无从下手，但通过正确的法是可以得到正确答案的，你准备好了吗?

SAT数学题中的一些代数题直接给出方程并要求您求解变量。

例如：

如果(k- x)/ 2 = k 且k = 2，则x的值是多少?

但是许多最棘手的问题都是数字问题，要求你根据给定的题写出一个等式。虽然并不是要求你去解方程，但你仍然需要确保方程式有效。

请看以下的SAT数学题：

上周五，比尔每小时都在吃ÿ根糖果棒，一共吃了3小时，桑迪每小时都在吃ž根糖果棒，一共吃了5小时。以下哪项代表比尔和桑迪星期五吃的糖果棒总数?

A)8yz

B)15yz

C)3y + 5z

D)5y + 3z

即使您不知道如何直接解开这个等式，您也可以选择数字并代入以查看哪个方程式有效。

所以，假如比尔吃了2根糖果棒，桑迪吃了5个。这意味着如果比尔每小时吃2根糖果棒吃了3个小时，他的总数是3×2 = 6根糖果棒。

同样，桑迪总共吃了25根糖果棒。25 + 6= 31，这意味着我们需要将y = 2和z =5代入上面的等式中。我们得出的答案必须等于31，而选项C是满足这一要求的答案选择。

方程组问题对学生来说是最难的，不仅要求学生了解如何正确设置方程式，还要知道如何解题。

请看以下SAT数学题：

三明治店以每份6.50美元的价格出售三明治，每瓶饮料只需2.00美元。该商店一天销售209份三明治和饮料的总收入为836.50美元。那天卖了多少三明治?

A)77

B)93

C)99

D)105

现在的是写出销售商品数量和收入的等式：

售出的商品：假设x =卖三明治的数量，y =饮料的数量，那么x + y = 209

同样，我们知道一天的商店总收入(836.50美元)和三明治(6.50美元)和饮料(2.00美元)的价格。将这些代入等式：

收入：6.50 x + 2 y = 836.50

花点时间在草稿纸上写下这些方程式，这样能让自己更清楚要解决的SAT数学题，甚至可以帮助你记住用来解x的正确数值。

提示：尝试代入值!在“已售出物品”等式的每一边乘以2：

2(x + y)=2(209)

得到新等式：

2 x +2 y =418

然后，从收入中减去已售出物品：

6.50 x +2 y =836.50

- (2 x + 2 y = 418)

得到一个更容易解的方程式：

4.5 x =418.50

将每一边除以4.5，得到x =(418.50/ 4.5)=93。

因此， B是正确答案!

当您不知道SAT代数题的答案时，可以在草稿纸上写出方程式。这样，用给出的值就可以算出正确答案。有时候，挑选数字并将它们代入等式也是有帮助的。

如果你需要提高代数分数，中加雅思·留学提供美国SAT考试课程，供你大量练习!

通过问题解决和数据分析解决SAT数学题

SAT数学题中的此类题目通常要求您以数学方式展示真实情况。其中涵盖统计分析、比例、概率、建模和真实数据。

你会碰到解决变化率等题目。您还需要知道如何对增长率等因素进行建模。尽管你在课堂上学到了些知识，但还是难免在考试时不会做。

有时，是可以通过简化题目来解决增长率的难题的。听起来好像难以置信?

我们来看一道SAT数学题：

假设每14年猴子的数量增加一倍。2016年初，猴子数量约计为20只。如果P代表2016年后n年的猴子数量，则下列哪个等式代表数量随时间变化而变化?

A)P = 14 + 20 n

B)P = 20 + 14 n

C)P = 20(2)^(14 n)

D)P = 20(2)^(n / 14)

一开始，就可以用零去代替每个答案选择中的n。马上就可以排除A，因为当n = 0时，这意味着时间并未变化，并且题目中表明初始总数量必须等于20。

从这里开始，您可以推断出未来几年可能发生的事情。如果猴子数量应该在14年内加倍，那么当n = 14时，P必须等于40。因此可以排除B。然后当你用n = 14代入指数函数时，一个最终等于40是选项D。在这里代入零可能看不出哪个是正确答案，但可以让你更接近答案，提高SAT数学题分数!

注意概率

您很可能会在问题解决和数据分析题型中碰到概率题目。要解决概率问题，您需要知道如何区分互斥和独立，非互斥事件之间的区别。

涉及互斥事件的问题似乎是学生最难解决的问题。“互斥”意味着如果一个事件发生，另一个事件就不发生。请记住，当事件满足这个条件时，您需要做一些补充才能找到正确的答案。

因此，当您碰到互斥事件A和B的SAT数学题时，缓一下，看看每个事件独立于另一个事件发生的概率。换句话说，分别找到P(A)和P(B)。

为了得到答案，可建立这样的等式：P(A或B)= P(A)+ P(B)。

进阶数学

不要让这个SAT 数学题的名字给吓倒了。当然，处理数据建模，操纵方程和简化多项式函数可能会令人生畏。虽然从表面上看，这些SAT数学题看起来确实具有挑战性，但关键在于知道如何简化。

对于每道数学题，您应该问自己，所讨论的函数是否是最简单的形式。这里用一个例子来说明：

假设题目是

(2 X ² ý - 4 ý ²+ 12 的xy ²) - (X ² ý + 9 XY ² - 6 ÿ ²)

并且题目要求您找到等效的表达式。

乍一看，这一串简直就是天书。但如果仔细观察，可以通过组合同类项来简化以上表达式。在这道SAT数学题中，2个X ² ÿ 和X ² ÿ 是同类项。4 ÿ ²和6 ÿ ²，以及12 xy ²和6 ÿ ²也是同类项。

做数学题的时候，您同样需要确定哪些数学运算可应用于某些类型的题目。

如果遇到用括号分隔起来的函数题，例如(ax + b)(bx + 7)，则可以应用乘法交换律来简化。

但SAT数学题必然会出一道复杂的多项式除法题，例如：

如果x > 5，以下哪一项相当于1 /((1 /(x + 4))+(1 /(x + 5)))?

A)(2 X +9)/(X 2 + 9 X =20)

B)(X 2 + 9X + 20)/(2 X 9)

C)2 X 9

d)X 2 + 9 X 20

现在，你可能会盯着这道题看，并想知道如何简化。但是碰到这样的SAT数学题，通常需要仔细研究分母并忽略其余的等式。如何简化分母?

最简单的方法是将以上等式乘以

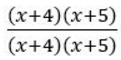
这样就可以去掉同类项。听起来有点熟?

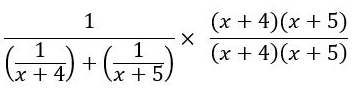
再继续看下一步分母是如何变化的：

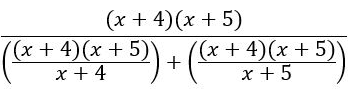
接下来，看一下分母中的两个分数。您可以将(x + 4)从个中的等式中分解出来，并将(x+ 5)中的因子分解出来。最后只剩下：

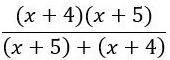
从这里开始，您可以在分子中应用箔规则，并在分母中组合同类项，再进一步简化：

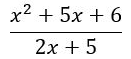
最终得出答案B!

如果您记住简化方程式、乘以或除以多项式的技巧，那么SAT数学题不一定是最难的。永远记得问自己：要怎样才能将这个题变成最简单的形式?