新航道留学背景提升丨海外科研远程-『理工』-数学前沿课题探究:构造性拓扑学分析
教授介绍
Vladimir Chernov
达特茅斯学院数学系终身教授
达特茅斯学院塞耶奖数学竞赛委员会主席
达特茅斯学院研究生招生委员会委员
微积分之外的数学概论课程发展委员会成员
达特茅斯大学本科生数学学会教师顾问
曾获达特茅斯学院秋季高 级教师奖
曾获西蒙斯基金会颁发 “数学家合作奖”
课题背景
拓扑学(Topology),是研究几何图形或空间在连续改变形状后还能保持不变的一些性质的学科。它只考虑物体间的位置关系而不考虑它们的形状和大小。在拓扑学里,重要的拓扑性质包括连通性与紧致性。你可以用任何你想要的方式拉伸、挤压和弯曲你的物体,但你不允许把它分开或把不同的部分粘在一起。例如,从拓扑学的观点来看,地球表面是一个球体,因为它可以变形成一个完美的圆形球体。事实上,地球表面不是圆的,所以从几何学的观点来看,它不是一个球体。同样地,从拓扑学的观点来看,一个咖啡杯和一个甜甜圈是一样的,因为你可以把一个变成另一个。
构造逻辑和更一般的构造数学处理对象,例如数字,它可以作为某些有限计算机算法的输出而生成。任何计算机算法都可以用它的二进制代码来表示,所以用这种方法可以得到的所有可能的数的集合都可以用正整数来枚举。根据定义,这意味着所有算法的集合,因此所有的构造数都是可计数的,所有有理数的集合也是可数的,但令人惊讶的是所有无理数的集合是不可数的。
课题内容
在这门课中,我们将着重于理解陈述并使用构造数学中的一些重要结果。我们还将涵盖“分析”和“拓扑”集的一些基本概念和定理。
参与本课程的学生将分成几个小组研究项目,以探讨在构造性世界中,分析和拓扑学中的一些基本定理的陈述在多大程度上得到了延续。
适合人群
对数学拓扑,几何图形感兴趣的高中生,本科生,研究生
修读数学专业,以及未来希望在应用数学,计算机科学,物理学,生物等领域从业的学生
具备微积分II, 或与此相当课程的学生优先
建议提前掌握一元函数积分,微分基础,基本计算机算法,二进制代码等专业知识
项目设置
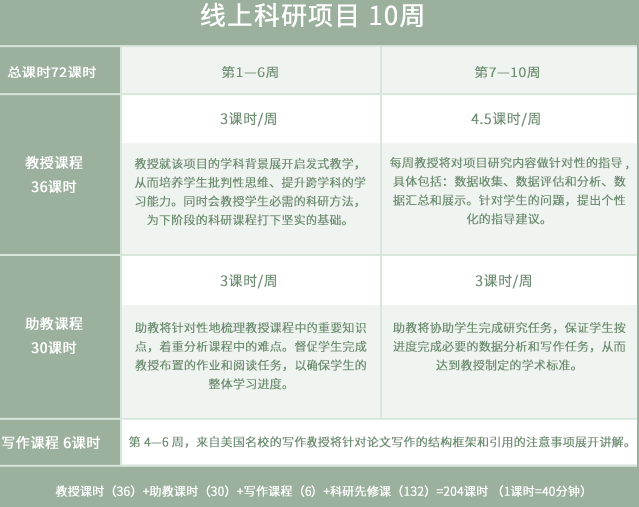
你将会得到
6周在线授课+4周在线小组科研(教授亲自论文辅导),教授全程参与为期10周
网申推荐信
学术评估报告
项目成绩单
论文成果








